
Le modèle de Wilson : clé de la gestion optimale de vos stocks
Le modèle de Wilson, aussi appelé EOQ (pour Economic Order Quantity), est une méthode de calcul mathématique permettant de connaître la fréquence et la quantité des commandes à passer auprès d’un fournisseur pour assurer une bonne gestion des stocks.
Bien que ce modèle soit souvent associé à l’approvisionnement en matières premières et à la gestion optimale des stocks, il convient de noter que la méthodologie de Wilson peut en réalité être appliquée à tout type de marchandise.
Formule du modèle de Wilson
Exposée à l’origine par l’ingénieur américain Ford Whitman Harris en 1913, ce n’est qu’en 1934 que le consultant R.H. Wilson réussit à développer la formule. Mais comment est calculé la quantité optimale d’une commande ?
A partir du niveau de demande d’un produit, du coût associé à la commande et du coût de stockage, il est possible de déterminer le volume de commande optimal. La formule mathématique est la suivante :
- Q= quantité optimale de la commande
- D= demande annuelle de la matière première concernée
- K= coût associé à chaque commande passée
- G= coût de stockage dans l’entrepôt d’une unité de produit pendant une période précise
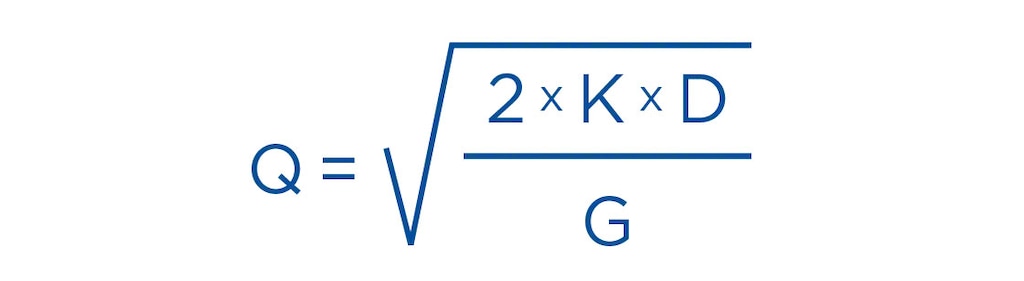
Applications et limites
Ce modèle mathématique vise à optimiser le volume d’achat de tout produit nécessaire, en précisant quand passer une commander à un fournisseur et en quelle quantité.
Grâce à cette information, et en prenant en compte le lead time et le stock de sécurité, il est également possible d’obtenir le point de commande (c’est-à-dire à quel moment passer chaque commande). La méthode de Wilson a pourtant certaines limites. En effet, cette méthode mathématique n’est applicable qu’aux entreprises pour lesquelles les deux conditions suivantes sont remplies :
- Une demande constante en matières premières tout au long de l’année
- Un prix d’achat du produit fixe dans le temps, sans fluctuations importantes tout au long de l’année.
Si le coût de la matière première varie en fonction de la saisonnalité, par exemple, cette formule mathématique devient inefficace, car elle ne tient pas compte de cette variable.
Par conséquent, cette méthode n’est conseillée que pour certaines entreprises où la demande et les coûts ne sont pas soumis à des variations importantes tout au long de l’année.
Avantages de la méthode
Pour les entreprises remplissant ces deux conditions, cette méthode mathématique garantit l’optimisation de la gestion des stocks. En effet, cette méthode présente les avantages suivants :
- Vous minimisez les coûts d’acquisition et de stockage.
- Vous évitez le surstockage, mais assurez un stock suffisant pour répondre à la demande.
- Vous connaissez la quantité exacte à acheter pour chaque commande.
- Vous évitez les ruptures de stock.
Exemple d’application du modèle de Wilson
L’entreprise imaginaire Orch Kork fabrique et distribue des bouchons en liège pour les entreprises viticoles locales. Pour assurer sa production annuelle de 10 000 unités, l’entreprise achète 1 000 kg d’écorce de chêne-liège tout au long de l’année.
Si chaque commande a un coût de 200 € incluant les frais de transport, et le coût de stockage du produit qui ne dépasse pas 2 000 € par an, quel est le volume de commande optimal ?
Dans cet exemple, la quantité optimale de commande, Q, est égale à la racine carrée du quotient (2*200*1000/2000), soit 14,14.
Orch Kork doit donc passer des commandes annuelles de 14 kg afin de disposer d’une quantité optimale d’écorce de chêne-liège pour produire des bouchons, évitant ainsi non seulement un surstockage de matière première, mais aussi d’éventuelles ruptures de stock. Par conséquent, l’entreprise doit passer 71 commandes annuelles de 14 kg pour disposer des 1 000 kg d’écorce de chêne-liège nécessaire à sa production.
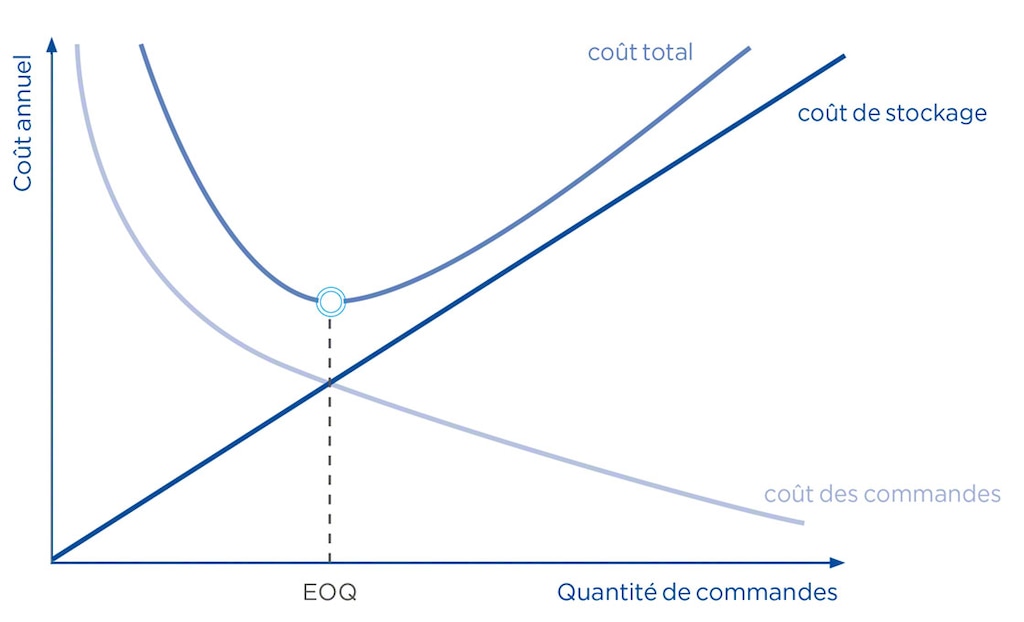
EOQ : minimiser ses coûts de stockage avec comme condition l’absence de saisonnalité
En conclusion, en appliquant le modèle de Wilson à la gestion de ses stocks, l’entreprise optimiserait ses commandes et minimiserait ses coûts de stockage et d’achat, mais en partant du principe que ce modèle n’est applicable que lorsque la demande et les prix sont constants tout au long de l’année. Le modèle étant inutile pour des scénarios plus complexes, dans ces cas, il est nécessaire de s’appuyer sur un logiciel de gestion d’entrepôt.
